函数图像小结

函数图像总结

一次函数

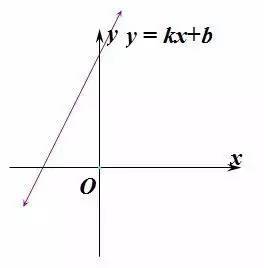
• 表达式：$y=kx+b$

  • $k$：斜率，k值越大则函数直线越往上升
  • $b$： 决定函数图像上移或下移

二次函数

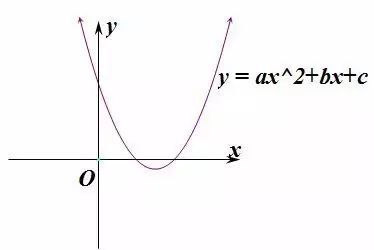
• 表达式：$y=ax^2+bx+c$

  • $a$：a值越大则函数开口越小，反之亦然；若a为负数开口向下
  • $b$：b和a共同决定对称轴的位置.当a与b同号时（即ab>0）,对称轴在y轴左；当a与b异号时（即ab<0）,对称轴在y轴右.
  • $c$：c决定抛物线与y轴交点.抛物线与y轴交于（0,c）

反比例函数

• 表达式：$y=/frac{k}{x}$

  • $k$：
    1. 当k>0时，图象分别位于第一、三象限，每一个象限内，从左往右，y随x的增大而减小；
    2. 当k<0时，图象分别位于第二、四象限，每一个象限内，从左往右，y随x的增大而增大。

指数函数

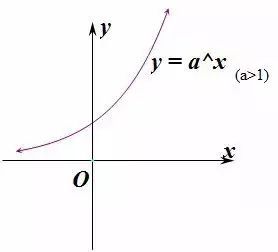
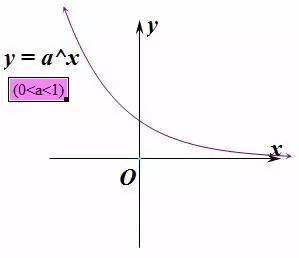
• 表达式：$y=a^x$

  • 在y轴右边“底大图高”；在y轴左边“底大图低”。底数为负数时图形向下

• 特性

  • $y=a^x$与$y=/frac{1}{a}^x$呈y轴对称

对数函数

• 表达式：$y=/log_a{x}$

  • 特性
    • 同底的对数函数与指数函数互为反函数。
    • 如果底数一样，真数越大，函数值越大。（a>1时）
    • 如果底数一样，真数越小，函数值越大。（0<a<1时）

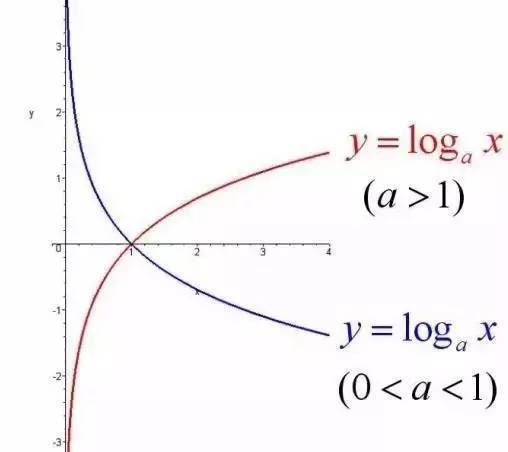
计算

对数计算

• $log_am+log_an=log_a{(m*n)}$
• $log_am-log_an=log_a{/frac{m}{n}}$
• $log_{a^m}{b^n}=/frac{n}{m}*log_ab$
  • $log_{a^m}b=/frac{1}m*log_ab$
  • $log_a{b^n}=n*log_ab$
• $a^{(log_aN)}=N$
• $log_ab=/frac{log_mb}{log_ma}$

由上可推导出一下公式

• $log_ab*log_ba=1$
• $lg5+lg2=1$
• $log_a{a^n}=n*log_aa=n$
• $log_ablog_bclog_cd…*log_ef=log_af$

算法常用函数

近似函数

描述	近似函数
调和级数求和	$H_N=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+…+\frac{1}{N} \approx lnN$
等差数列求和	$1+2+3+4+…+N\approx\frac{N^2}{2}$
等比数列求和	$1+2+4+…+N\approx2N-1\approx2N,其中N=2^n$
斯特灵公式	$lgN!=lg1+lg2+lg3+…+lgN\approx NlgN$
二项式系数	$\approx\frac{N^k}{k!},其中k为小常数$
指数函数	$(1-\frac{1}{x})^x\approx\frac{1}{e}$